 こんにちは!AX研究室のロベルト・フバチです。
こんにちは!AX研究室のロベルト・フバチです。
近年、機械学習を流体力学の問題に応用する研究が注目を集めています。
その中でもPhysics-Informed Neural Networks(PINN)は、データに基づく手法と物理法則を組み合わせる点が大きな特徴であり、少量のデータでも物理現象を再現できる可能性を持っています。PINNの概要については、以前の投稿の一つで紹介いるのでそちらをご覧ください。
本ブログでは、公開されているCFDデータセットWindsorML(Ashton et al., 2024)を用いて、自動車周りの乱流空気流れのシミュレーションを行った事例を紹介します。対象は、WindsorMLデータセットに含まれる多数のシミュレーションケースの一つであるrun_0ケースです。
WindsorMLは、自動車空力を高精度に解析することを目的として構築された大規模かつ高品質なデータセットですが、その規模の大きさから、すべてのデータをそのまま利用することは実際には容易ではありません。
そこで本検討では、WindsorMLデータのごく一部のみを使用した場合に、PINNモデルがどの程度流れ場を再現できるのかを検証しました。元データは約2億点ですが、ベースライン用のデータとして約200万点(約1%)を抽出し、PINNの学習にはさらに少量の50,000点(約0.025%)を用いました。
この記事で分かること:
-
約2億点のデータセットに対して、学習点50,000点(約0.025%)という極少データでも、PINNで流れ場をどこまで再現できるか
-
限られた観測点で学習した場合に、再現しやすい領域/誤差が出やすい領域がどこに現れるか
-
少量データ学習を前提にしたときの、(本記事で用いた)学習設定・前処理が結果にどう影響し得るか
乱流とレイノルズ応力
乱流とは、流体(液体または気体、例えば空気)が不規則に動く状態を指し、その中では多数の渦が発生します。これらの渦は、急激で不規則な速度変化(変動)を引き起こし、これをフラクチュエーションと呼びます。これらの変動の平均的な効果は、いわゆるレイノルズ応力によって表現することができます。レイノルズ応力は、直感的には、乱流によって生じる流体内の追加的な「摩擦」として捉えることができます。
このような流体の運動は、乱流流れまたはタービュレント流れとも呼ばれます。
CFDデータセットWindsorMLには、自動車周りの乱流空気流れを対象としたシミュレーション結果が含まれています。これは、データの中に乱流の影響、すなわちレイノルズ応力に関する情報も含まれていることを意味します。そのため、シミュレーションを行う際には、これらの応力を適切に評価・推定する必要があります。
理論的には、速度・圧力・レイノルズ応力を同時に予測する一つの大規模なPINNを用いることも可能です。しかし、実際にはこのような手法は実装が難しく、学習が不安定になるなどの問題が起こりやすくなります。そこで本検討では、別のアプローチを採用しました。
具体的には、RNetと呼ばれる追加のニューラルネットワークを導入し、主となるPINNの学習に先立ってRNetを事前に学習させました。RNetの役割は、空間内の任意の点におけるレイノルズ応力の値を推定(補間)することです。レイノルズ応力を別ネットワークで近似して固定することで、PINN側は「速度・圧力」に集中でき、同時最適化の難しさ(不安定さ)を避けられ、乱流の影響を間接的に取り込むことが可能になります。
Physics-Informed Neural Networks(PINN)
本稿では、Physics-Informed Neural Networks(PINN)を用いた実験を行いました。
PINNは、物理法則を表す方程式を学習過程に直接取り入れることを特徴とするニューラルネットワークです。しかし、物理方程式のみに基づいてPINNを安定して学習させることは、実際には容易ではありません。
そのため、PINNの学習においては、データ駆動型アプローチとして、
CFDシミュレーションから得られたデータを併用することが一般的です。
その結果、PINNモデルは学習の過程において、次の2つの重要な点を同時に考慮します。
- 予測された速度場および圧力場が、与えられたデータとどの程度一致しているか
- 空気の流れを記述する物理方程式(Navier–Stokes 方程式/RANS方程式)を
どの程度満たしているか
このような手法により、次のような利点が得られます。
- ネットワークの学習に必要なデータ点数を抑えることができる
- 解の汎化性能を向上させることができる
PINNの学習は、Adam最適化アルゴリズムを用いて100,000回のイテレーションで実施しました。
PINNネットワークのアーキテクチャ
PINNモデルは、入力として三次元の空間座標(x, y, z)を受け取り、空気の流れに関連する4つの物理量を出力します。
- 速度ベクトルの3つの成分(u, v, w)
- 圧力(p)
ネットワークのアーキテクチャは、以下の要素から構成されています。
- 6層の全結合型隠れ層
- 各層に64個のニューロン
- 活性化関数としてTanhを使用
RNet
RNetの役割は、空間内の位置に基づいてレイノルズ応力を予測することです。
RNetは、以下の特徴を持つ通常のニューラルネットワークとして学習されました。
- 物理方程式を直接課さず、
- データのみに基づいて学習
RNetの学習には、次の2つのアプローチを用いました。
- 全データセットを用いた学習
(この場合、WindsorMLデータセットからランダムに選択した2,000,000点を使用。詳細は後述) - 学習用データのみを用いた学習
(50,000点の学習データを使用)
RNetを全データセットで学習させることは、本稿の基本的な考え方である「少量のデータを用いた学習」という方針と完全には一致していません。
それにもかかわらず、この学習を行ったのは、レイノルズ応力を可能な限り正確に予測できる基準(ベースライン)を得るためです。
この基準と比較することで、RNetを学習用データのみに基づいて学習させた場合との違いを明確に評価することができます。
RNetの学習には、Adam最適化アルゴリズムを使用しました。
RNetネットワークのアーキテクチャ
RNetは 全結合型ニューラルネットワークであり、入力として空間座標 (x, y, z) を受け取り、6成分のレイノルズ応力を出力します。
RNetのアーキテクチャは、以下の構成となっています。
- 4層の隠れ層
- 各層に128個のニューロン
- 活性化関数としてTanhを使用
データ
なぜWindsorMLなのか?
WindsorMLデータセットは、以下の理由から特に興味深いものです。
- 自動車の現実的な空力特性を詳細に記述している
- CFDとAIを組み合わせたハイブリッド手法の検証に非常に適している
データの内容
WindsorMLデータには、主に以下の情報が含まれています。
- 三次元の速度場
- 圧力分布
- レイノルズ応力
- 車両のジオメトリを含む計算領域全体
学習用・テスト用データセット
WindsorMLの元データは、自動車周りの計算領域において約2億点の情報を含んでおり、非常に大きなメモリ負荷を伴います。
本稿では、実験を行うために200万点をランダムに抽出し、それらを以下のように分割しました(図1)。
- 学習用データ:50,000点
- テスト用データ:1,900,000点
- コロケーション点:50,000点
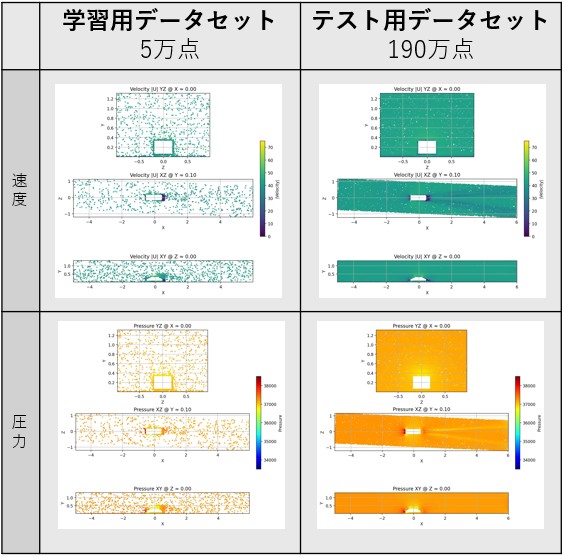
図1.モデルの学習およびテストに用いられるCFDデータの可視化。各データセットの可視化結果は、3 つの幾何学的断面、すなわちYZ面(X=0)、XZ面(Y=0.1)、およびXY面(Z=0)において示されている。X 方向の寸法が他の方向よりも大きいため、YZ 断面は拡大して表示している。各断面に見られる白い領域は、自動車の形状を表しています。データはWindsorMLデータセット(Ashton et al., 2024)から直接取得されたものであり,ライセンスはCC BY-SA 4.0です。
コロケーション点とは?
コロケーション点は、流れを記述する微分方程式から直接生じる誤差を評価するために用いられます。
学習中は、これらの点について空間座標(x, y, z)のみを使用し、速度・圧力・レイノルズ応力といった物理量はデータベースから取得しません。
コロケーション点の選択には、次の2つの方法を採用しました。
- fixed:学習開始前に50,000点を選択し、学習中は変更しない方法
- random:各エポックごとに、計算領域全体から50,000点をランダムに選択する方法
ランダムサンプリングは、PINNモデルの汎化性能を向上させ、流れ場をより正確に再現することが期待されます。
学習データの前処理
シミュレーションで使用したすべての物理量(位置、速度、圧力、レイノルズ応力)は、無次元化して扱いました。
無次元化の方法については、過去のブログ記事で説明していますので詳しくはそちらをご覧ください。
さらに、一部の計算では、空間座標を[-1, 1]の範囲に正規化しました。これは、ニューラルネットワークにおける勾配消失問題を緩和することを目的としています。
結果
表1.RMSE誤差の値に基づく、異なるPINNモデルの精度比較。モデル名の表記規則:R200/R5はRNetの学習点数(200万点/5万点)、f/rはコロケーション点の選択方法(fixed/random)、y/nは座標正規化の有無(yes/no)を表します。
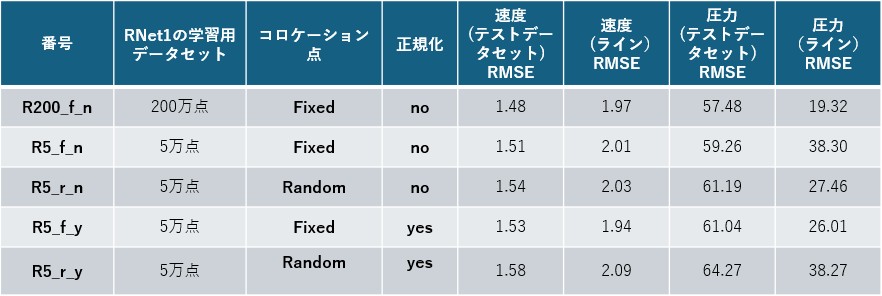
今回得られた、異なるPINNモデルの計算結果を表1および図2、図3に示します。表1のRMSEから、最良だったのはR200_f_nであり、RNet精度(レイノルズ応力推定の質)がPINN性能に強く影響することが分かります。一方、座標正規化やコロケーション点の選び方の効果は条件依存でした。
図2は、自動車周りのジオメトリに対して選択したいくつかの断面における速度場および圧力場を示している。図1に示したテストデータとの比較から、PINNモデルの結果は参照データと良好な定性的一致を示しており、PINNモデルが流れ場構造の主要な特徴を適切に再現できていることが確認できる。
図3では、PINNによる計算結果とテストデータとの比較を行いました。比較は、X=0、Z=0で定義される測定線に沿って行い、Y座標のみを変化させています。
この測定線上の点は等間隔に配置されていますが、Y座標の特定の範囲では点の間隔が大きくなっています。これは、その領域に自動車のジオメトリが存在し、計算点が存在しないためです。
この図から、PINNモデルは流れが最も複雑となる車体近傍において、速度および圧力の分布を非常に高い精度で再現することが難しいことが分かります。
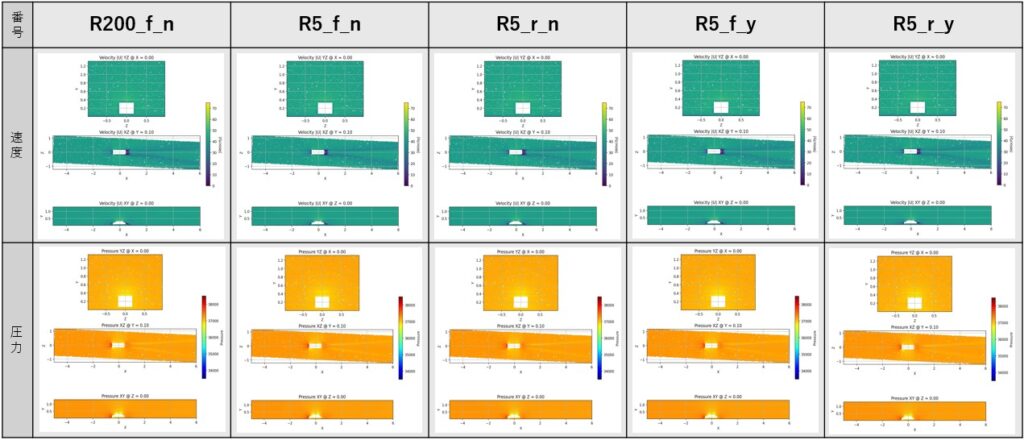
図2.WindsorML(Ashton et al., 2024)を用いて学習したPhysics-Informed Neural Network(PINN)による,テストデータ点に対する予測結果。各モデルの結果は、3つの幾何学的断面で示されています。YZ 面(X=0)、XZ面(Y=0.1)、およびXY面(Z=0)です。X方向の寸法が他の方向よりも大きいため、YZ断面は拡大表示しています。各断面に見られる白い領域は、自動車の形状を表しています。
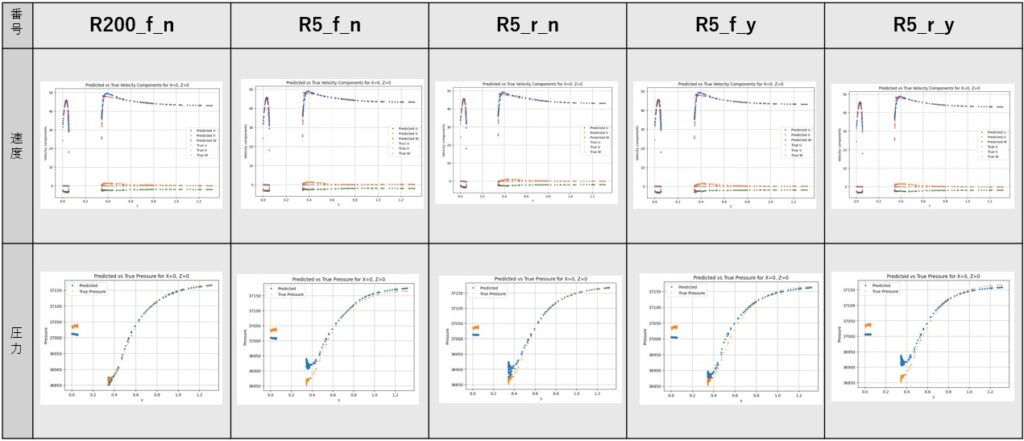
図3 測定線(X=0、Z=0)におけるPINNの計算結果とテストデータの比較。速度については、座標系(x, y, z)に対応する 3 つの速度成分(u, v, w)を示している。このグラフに示されているテストデータには、真の圧力(True Pressure)および 真の速度成分(True u、True v、True w) が含まれています。テストデータはWindsorMLデータセット(Ashton et al., 2024)から直接取得されたものであり, ライセンスはCC BY-SA 4.0です。
ここで用いるモデル名の表記は、R200/R5=RNet学習点数(200万/5万)、f/r=コロケーション点(fixed/random)、y/n=座標正規化(yes/no)を表します。表1には、PINNモデルの計算結果とテストデータとの差を表すRMSE誤差を示しています。RMSEは、テストデータ全体を用いた場合と、測定線上の点のみを用いた場合の2通りで算出しました。
RMSEの値から、最も良好な結果を示したのはR200_f_nバージョンのPINNモデルであることが分かります。このモデルでは、2,000,000点を用いて学習したRNetを使用しています。これは、学習データ数が多いほど、レイノルズ応力をより正確に推定できるためであり、予想と一致する結果です。したがって、RNetによるレイノルズ応力のより高精度な近似は、PINNモデルの性能向上につながるといえます。
次に良好な結果を示したのは、R5_f_yバージョンのモデルです。このモデルでは、空間座標(x, y, z)の正規化を行い、RNetは 学習用データのみ(50,000点)を用いて学習されています。
これら 2 つのモデル(R200_f_nとR5_f_y)では、他のモデルと比較して、車体近傍における圧力分布の再現性が向上していることも確認できます(図3)。
本稿で提示された結果 (表1など) では、空間座標を正規化し、コロケーション点をランダムに選択することがPINNトレーニング・プロセスで常に有利になるとは言えませんでした。
空間座標の正規化を行った場合には、コロケーション点を固定(fixed)して選択したR5_f_y モデルが、より良い結果を示しました。
一方、空間座標の正規化を行わない場合には、コロケーション点をランダム(random)に選択した R5_r_nモデルにおいて、車体近傍の圧力分布がより良く再現されました。
まとめ(結論)
本稿で示した結果から、比較的シンプルな PINNネットワーク構造で、空気流れの主要な特徴を再現することができました。これは、限られた学習データを用いた場合でも成り立ちます。
一方で、自動車表面近傍の領域は、車両形状の設計などにおいて特に重要であるにもかかわらず、高精度な再現が難しい領域であることも明らかになりました。
結果を改善するための最も単純な方法の一つとして、車体表面近傍から取得した、速度・圧力・レイノルズ応力の情報を含む学習点を増やしてPINNを学習させることが有効であると考えられます。
データの出典:
本稿で使用したWindsorMLデータセットについては以下をご覧ください。
Ashton, N., Angel, J. B., Ghate, A. S., Kenway, G. K. W.,
Long Wong, M., Kiris, C., Walle, A., Maddix, D. C., Page, G. (2024):
WindsorML: High-Fidelity Computational Fluid Dynamics Dataset for Automotive Aerodynamics
https://arxiv.org/abs/2407.19320
データセット公開ページ:
https://huggingface.co/datasets/neashton/windsorml
ライセンス:
Creative Commons 表示–継承4.0 国際(CC BY-SA 4.0)
https://creativecommons.org/licenses/by-sa/4.0/





