 こんにちはAX研究室のロベルト・フバチです。この投稿では、PINN(Physics-Informed Neural Networks、物理情報ニューラルネットワーク)を用いて、障害物の周囲を流れる流体のシミュレーション方法を紹介します。
こんにちはAX研究室のロベルト・フバチです。この投稿では、PINN(Physics-Informed Neural Networks、物理情報ニューラルネットワーク)を用いて、障害物の周囲を流れる流体のシミュレーション方法を紹介します。
PINNの概要については、以前の投稿の一つで紹介しました。一般的に、これらのネットワークは、自然界や産業界で発生する現象を記述する偏微分方程式を解くために使用されます。
そのような現象の一つが流体の流れであり、これは液体や気体の運動を研究する「流体力学」という分野の対象です。「流体」という用語は液体と気体の両方を指し、固体とは異なり、自由に流れたり形を変えたりする性質があります。
流体が障害物にぶつかると、その背後にカルマン渦と呼ばれる渦が発生することがあります。これらの渦は規則正しく並び、特徴的なパターンを形成します。この現象は、例えば風が旗のポールを通過する際に、旗が規則的に揺れることで観察できます。同様の渦は、島や岩の背後を流れる水、あるいは山地の周囲を流れる空気中の雲にも見られます。
このような流れをシミュレーションするために、PINNはナビエ–ストークス方程式や連続の式などの微分方程式(図2)を利用します。たとえば、管内の層流のような単純な流れでは、これらの方程式に含まれる物理法則だけでPINNが流体の速度分布を効果的に予測できます。
しかし、カルマン渦のような非定常で非線形性の強い複雑な流れでは、従来の数値流体力学(CFD)による完全な再現は計算コストや数値安定性の観点から困難です。一方、限られた測定点での観測データのみでは、流れ場全体の詳細な把握は不可能です。PINNsはこの課題に対し、ナビエ・ストークス方程式などの物理法則を損失関数に組み込むことで、少ない観測データからでも物理的に一貫した流れ場を学習・予測することができます。具体的には、測定された速度や圧力データと物理方程式の制約を同時に満たすよう学習することで、観測点以外の領域についても信頼性の高い流れ場情報を補間・外挿できます。このように、実験データと物理モデリングを統合したアプローチにより、カルマン渦の詳細な時空間構造を効率的に把握することが可能になります。
本稿では、トレーニングデータの量や準備方法が、カルマン渦PINNモデルの精度にどのように影響を与えるかを示します。
問題の説明
問題を簡略化するために、このブログ記事では2次元の流れに焦点を当てます。このような単純化は、流体が流れる障害物が長く、その端で起こる現象が全体の流れに大きな影響を与えない場合に意味があります。このような状況では、長い矩形断面の柱の周囲の流れをシミュレーションする代わりに、その断面に対応する長方形の周囲の流れを検討するだけで十分です(図1参照)。
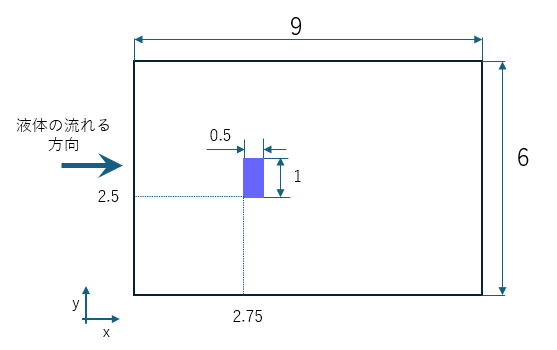
図1.この図はカルマン渦を伴う流れのシミュレーションに使用された形状を示しています。中央の青い長方形は、流体がその周囲を流れる障害物です。寸法は無次元の形で示されています。
図2には、2次元系における流体の流れを記述するナビエ–ストークス方程式と連続の式が示されています。これらの方程式については、本記事の理解に必要ないため、ここでは詳細に説明しません。
しかし、これらの方程式に登場する物理量(距離、速度、圧力、時間など)はすべて無次元化されており、単位を持ちません。この処理によって、方程式はより一般的な形となり、コンピュータ解析において扱いやすくなります。
また、ナビエ–ストークス方程式に現れる重要なパラメータの1つに「レイノルズ数」があり、これも無次元量です。レイノルズ数は流れの性質(例えば層流か乱流か)を表します。
このブログの以降の部分では、すべての量はこの無次元形式で表記されます。

図2.2次元無次元ナビエ–ストークス方程式および連続の式。記号の説明:u,vはそれぞれ x,y 方向の無次元速度、p は無次元圧力、x,y は無次元座標、t は無次元時間、D は特性長さ(代表的な物理的寸法)、Uは特性速度(代表的な速度スケール)、ρ は流体の密度、μ は流体の粘性係数(動粘性)、Re (レイノルズ数)は慣性力と粘性力の比を表す無次元数。ここで添字 dim は次元を持つ物理量を示す。
PINNを用いた流れのシミュレーション実施手順
このブログで紹介するPINNの学習とテストのプロセスは、4つのステップで構成されています(図3参照):
参照データの作成、トレーニングデータの選定、モデルの学習、そしてその性能の評価です。
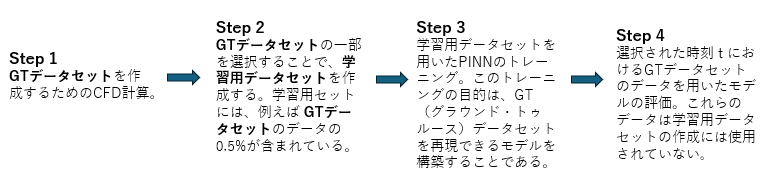
図3.データ作成、学習用データの選定、モデルの学習、評価の4段階で構成されるPINNの学習と検証のプロセス。
ステップ1:データセットの準備 — 参照データ(GT:グラウンドトゥルース)
実験データが入手できなかったため、PINNの学習には、事前に行われたカルマン渦を含む流体の数値シミュレーション結果を使用しました。
このシミュレーションは、ニューラルネットワークを用いず、従来の数値流体力学(CFD)の手法によって実行されました。使用されたコードは「PythonでNavier-Stokes方程式を解いてカルマン渦をシミュレーションする」のQiitaブログからのものです。(感謝)
このシミュレーション(レイノルズ数 Re = 100 にて実施)は、時刻 t = 0 から t = 100 にかけて流体の挙動がどのように変化するかを示しています。初期状態(t = 0)では流体は静止していますが、時間の経過とともに流速が増加し、特徴的なカルマン渦が現れます。
つまり、流れは初期段階と後の段階で異なります。最初は「立ち上がり(遷移)」があり、その後に渦が発生します。このため、PINNの学習に使用するデータの一貫性を保つために、完全に渦が発達した後のシミュレーション部分のみを使用することにしました。具体的には、時刻 t = 50 以降のデータを用いました。
数値計算の結果、空間(x, y)の5551地点で、時間(t)とともに変化する流体の速度と圧力(u, v, p)の値を含むデータセットが作成されました。シミュレーションは時刻 t = 50 から t = 100 までの1000タイムステップで構成されており、全体で5,551,000行のデータが得られました。各行はそれぞれ一意の座標 (x, y, t) に対応しています。
このデータセットは流れの全体的な挙動を詳細に記述しており、PINNモデルの出力と比較するための基準(リファレンス)として扱われます。このブログでは、このデータセットを「GTデータセット(Ground Truth)」と呼ぶことにします。
ステップ2:トレーニングデータの選定
次のステップでは、GTデータセットを用いて学習用データセットを準備しました。これらのデータは、2つの方法で生成されました。
「ランダム」 方式 — 全データベースからランダムに指定数の行を選び、それをPINNの学習に使用しました。以下の3種類のサイズの学習データセットが作成されました:
27,755行(GTデータセットの0.25%)
13,877行(GTデータセットの0.25%)
6,938行(GTデータセットの0.125%)
「選択された点からの抽出」 方式 — シミュレーション領域内の特定の点に対応するデータのみを選択しました。図4に示された25の制御点に基づいてデータセットを作成しました。この方法で得られたデータセットのサイズは25,000行(GTデータセットの0.45%)でした。このようなデータの選び方は、特定の場所に配置されたセンサーで流れ情報を取得する実際の状況に相当します。
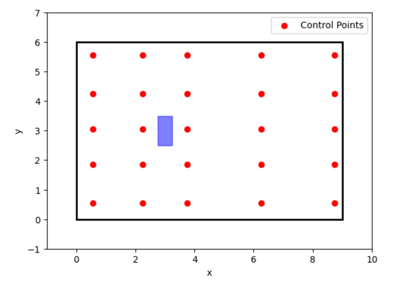
図4. シミュレーション領域における制御点の配置(「選択された点」手法)。各点の座標は、x_list(x 成分)および y_list (y 成分)として示されています:x_list = [0.55, 2.25, 3.75, 6.25, 8.75]、y_list = [0.55, 1.85, 3.05, 4.25, 5.55]。データセットは、図に示された点における流体の速度成分と圧力の値を基に作成されました。
ステップ3:モデルの学習(トレーニング)
ニューラルネットワークのアーキテクチャ(PINNを含む):
ニューラルネットワークは4つの隠れ層で構成されており、それぞれの層には64個のニューロンがあり、活性化関数としてTanhが使用されています。
このネットワークは、空間座標と時間(x, y, t — 3つの入力)をもとに、流体の速度と圧力の値(u, v, p — 3つの出力)を予測します。
損失関数:
損失関数は、次の式に基づいて定義されます:
Total_loss = lambda_1 · pde_loss + lambda_2 · data_loss
• pde_loss – PINNによって予測された速度および圧力が、ナビエ–ストークス方程式および連続の式を完全には満たしていないことによる損失項。
• data_loss – PINNによる予測値と、トレーニングデータ中の対応する速度および圧力の値との差に基づく損失項。
PINNを用いたシミュレーションでは、lambda_1 = 1 および lambda_2 = 1 の値が使用されました。
比較のために、lambda_1 = 0 のケースでもシミュレーションが行われました。これは、流れを記述する物理方程式を考慮しない通常のニューラルネットワークに相当します(つまり、PINNではないNN)。
最適化手法と学習パラメータの選定:
モデルの学習にはAdamオプティマイザが使用されました。最も良い結果は、学習率が0.001のときに得られました。最高の精度を達成するために、なんと40万エポックにおよぶ非常に長いトレーニングプロセスが選択されました。PINNネットワークのトレーニングの目的は、GTデータセットの再現にあります。そのため、モデルの過学習によるエラーは、従来のニューラルネットワークのように深刻な問題とは見なされません。従来のネットワークでは、トレーニングデータへの過剰適合が一般化能力の喪失につながる可能性があります。
ステップ4:学習済みPINNモデルの性能評価
学習プロセスの完了後、PINNは指定された t, x, y の値から u, v, p の値を計算できるようになります。
モデルの性能を評価するために、GTデータセットからのデータを用いてテストを行いました。評価には、3つの特定の時刻(t = 51、t = 75、t = 99)のデータを使用しました。これらのデータは意図的にトレーニングデータセットから除外され、テストデータとしてのみ使用されました。各テストセットは、空間内の5551地点(x, y)を含んでいます。
精度の指標としては、PINN(または通常のニューラルネットワーク)によって予測された u, v, p の値と、CFDシミュレーション(GTデータセット)で得られた結果との間の平均二乗誤差(MSE)が使用されました。
ケース1:ランダムに抽出されたデータによる学習
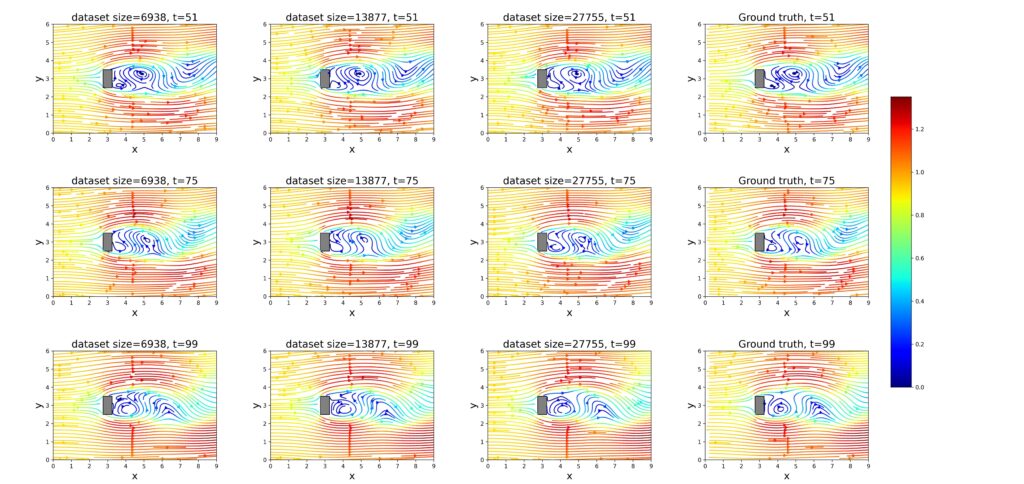
図5. PINNモデルによるシミュレーション結果とGTデータセットとの比較 — ランダムデータセットの場合。
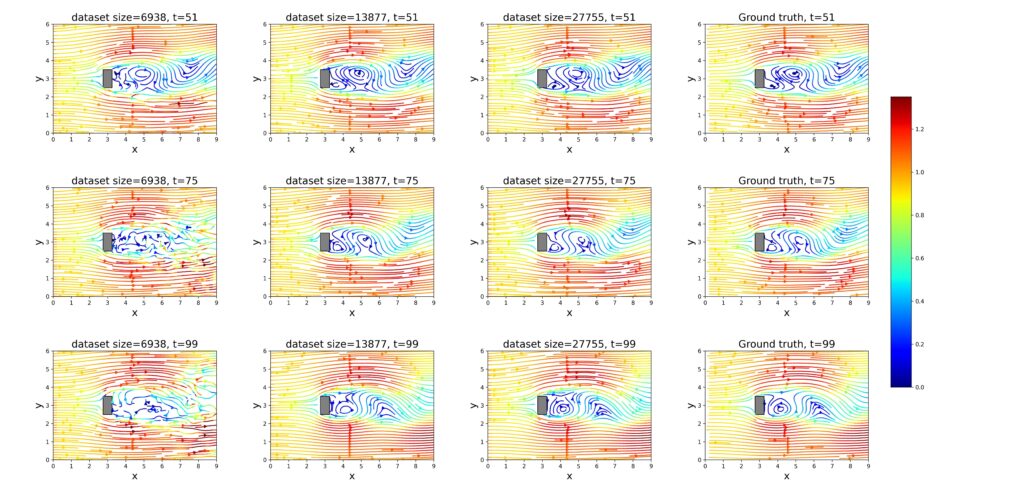
図6.通常のニューラルネットワークによるシミュレーション結果とGTデータセットのデータとの比較 — ランダムデータセットの場合。
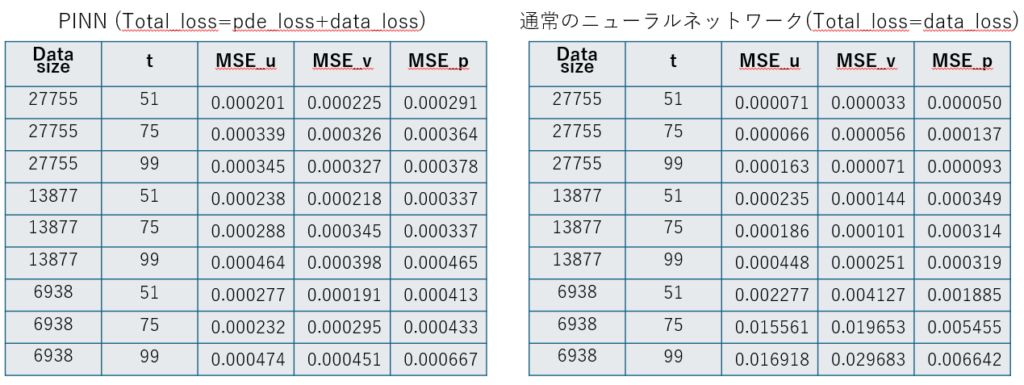
図7.各シミュレーションにおける平均二乗誤差(MSE)の値 — ランダムデータセットの場合
このケースにおけるシミュレーション結果と、それに対応する平均二乗誤差(MSE)の値は、図5、図6、および図7に示されています。
学習データとして27,755行および13,877行を含むデータセットを使用した場合、従来型のニューラルネットワークはPINNよりも低いMSE値を達成しました。これは、トレーニングデータへの適合度が高いことを示唆しています。ただし、これらのデータはCFDシミュレーションに基づいており、数値的な誤差を含んでいる可能性がある点に注意が必要です。
通常のニューラルネットワークとは異なり、PINNは単に入力データを再現するだけでなく、ナビエ–ストークス方程式や連続の式といった物理法則も考慮に入れています。そのため、たとえ形式的なMSEが高かったとしても、流体力学的観点からはより信頼性の高い結果を提供できます。
さらに、PINNはトレーニングデータセットのサイズが小さくなっても高い耐性を示しました。データ量にかかわらずMSEの値は安定していました。一方で、従来型のネットワークでは、利用可能なデータが少なくなると精度が大きく低下しました。
ケース2:選択された点からのデータによる学習
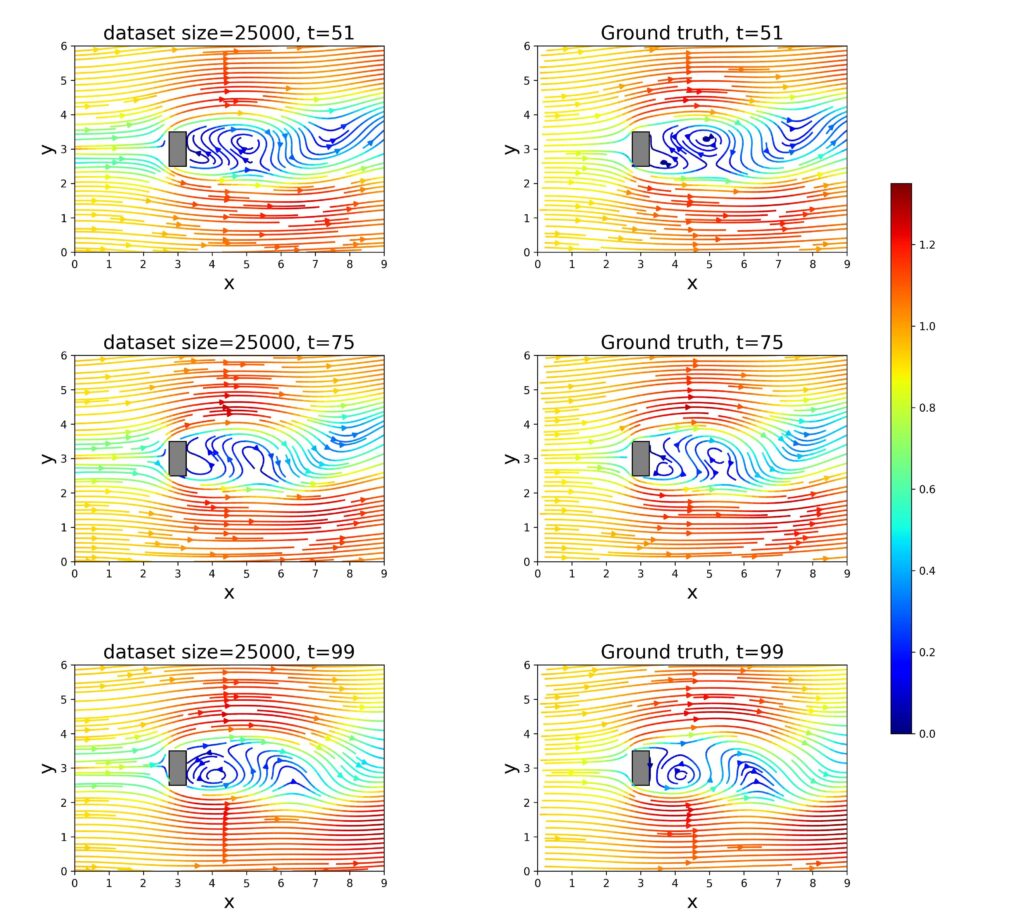
図8. PINNモデルによるシミュレーション結果とGTデータセットとの比較 — 「選択された点」手法で生成されたデータセットの場合。
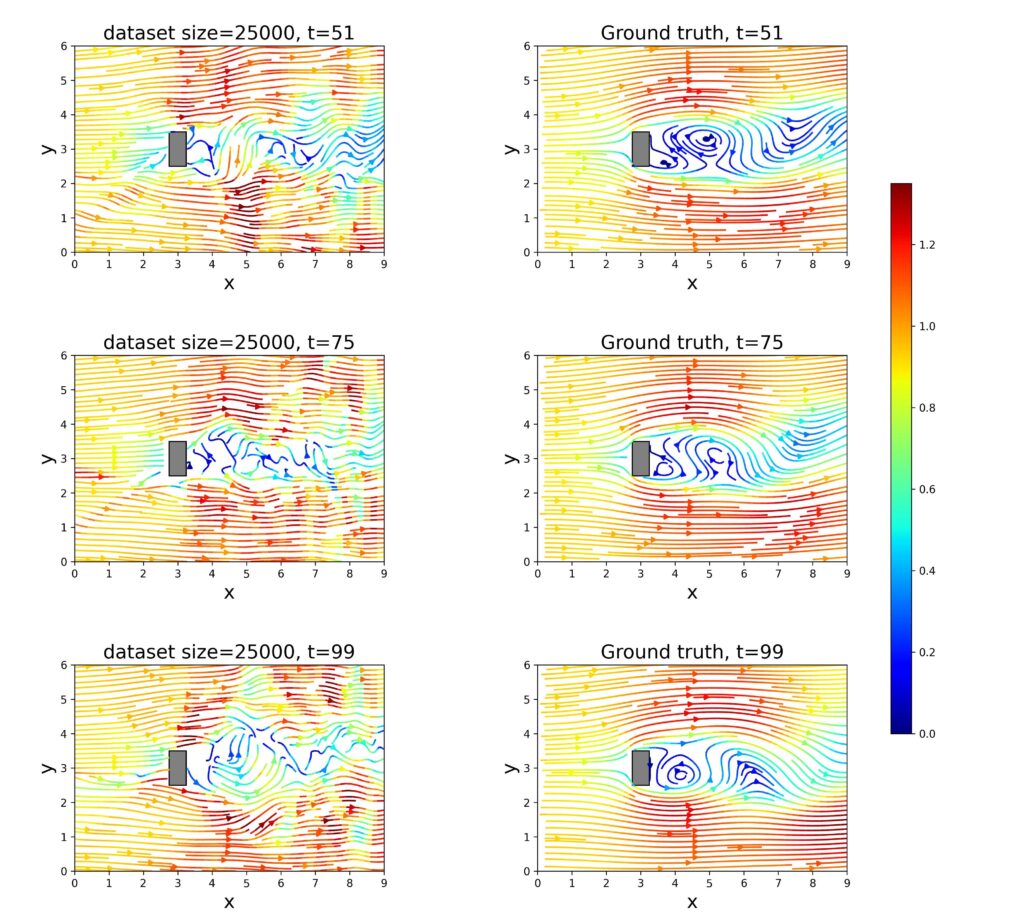
図9.通常のニューラルネットワークによるシミュレーション結果とGTデータセットのデータとの比較 — 「選択された点」手法で生成されたデータセットの場合。

図10.各シミュレーションにおける平均二乗誤差(MSE)の値 — 「選択された点」手法で生成されたデータセットの場合。
このシナリオでは、図8、図9、および図10に示された結果に対して、「選択された点」手法で生成されたデータが使用されました。これは、流れに関する情報が特定の場所に配置されたセンサーによって収集される現実の状況を模倣しています。
結果は全体的にランダム抽出法よりも劣っており、ランダム法の方がGTデータセット全体の特徴をよりよく反映していることがわかります。
しかし、このような困難な条件下でも、PINNは流れの主要な特徴を再現する能力を維持しており、誤差がある中でも有効に機能しました。
これは、PINNが空間的に限られた情報からでも測定データをうまく一般化・解釈できることを示しています。
一方、通常のニューラルネットワークは大きく性能が低下し、予測精度が低く、流れの特徴を正しく再現することができませんでした。
まとめ
PINN(物理情報ニューラルネットワーク)は、物理方程式を考慮することで、データが限られていたりノイズが含まれていたりしても、実際の流れ現象をより正確に再現することができます。
従来のニューラルネットワークとは異なり、PINNはトレーニングデータの準備方法に依存せず、高い精度の結果を維持します。
この特性により、PINNは測定データが不完全または分散しているような工学的応用において、特に価値のある手法といえます。







