こんにちは!AX研究室のロベルト・フバチです。
こんにちは!AX研究室のロベルト・フバチです。
近年、機械学習を流体力学の問題に応用する研究が注目を集めています。
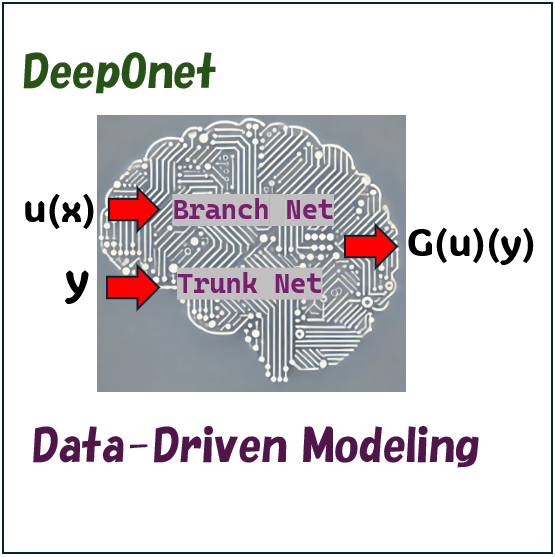
その中でもPhysics-Informed Neural Networks(PINN)は、データに基づく手法と物理法則を組み合わせる点が大きな特徴であり、少量のデータでも物理現象を再現できる可能性を持っています。PINNの概要については、以前の投稿の一つで紹介いるのでそちらをご覧ください。
本ブログでは、公開されているCFDデータセットWindsorML(Ashton et al., 2024)を用いて、自動車周りの乱流空気流れのシミュレーションを行った事例を紹介します。対象は、WindsorMLデータセットに含まれる多数のシミュレーションケースの一つであるrun_0ケースです。
WindsorMLは、自動車空力を高精度に解析することを目的として構築された大規模かつ高品質なデータセットですが、その規模の大きさから、すべてのデータをそのまま利用することは実際には容易ではありません。
そこで本検討では、WindsorMLデータのごく一部のみを使用した場合に、PINNモデルがどの程度流れ場を再現できるのかを検証しました。元データは約2億点ですが、ベースライン用のデータとして約200万点(約1%)を抽出し、PINNの学習にはさらに少量の50,000点(約0.025%)を用いました。
この記事で分かること:
-
約2億点のデータセットに対して、学習点50,000点(約0.025%)という極少データでも、PINNで流れ場をどこまで再現できるか
-
限られた観測点で学習した場合に、再現しやすい領域/誤差が出やすい領域がどこに現れるか
-
少量データ学習を前提にしたときの、(本記事で用いた)学習設定・前処理が結果にどう影響し得るか

 こんにちはAX研究室のロベルト・フバチです。この投稿では、PINN(Physics-Informed Neural Networks、物理情報ニューラルネットワーク)を用いて、障害物の周囲を流れる流体のシミュレーション方法を紹介します。
こんにちはAX研究室のロベルト・フバチです。この投稿では、PINN(Physics-Informed Neural Networks、物理情報ニューラルネットワーク)を用いて、障害物の周囲を流れる流体のシミュレーション方法を紹介します。